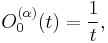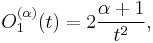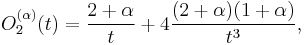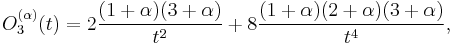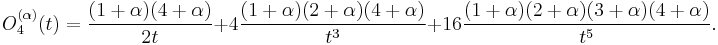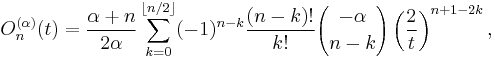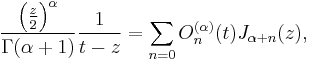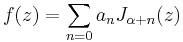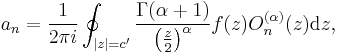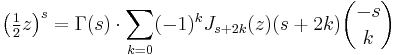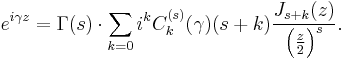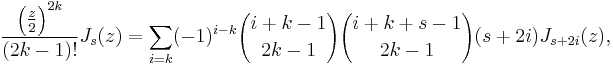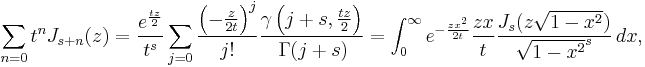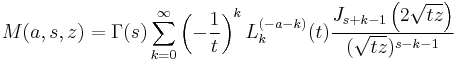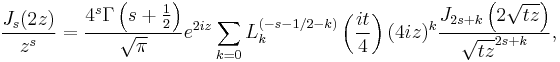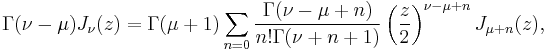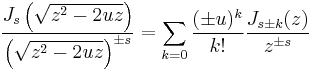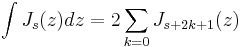Neumann polynomial
In mathematics, a Neumanns polynomial, introduced by Carl Neumann for the special case 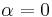 , is a polynomial in 1/z used to expand functions in term of Bessel functions.[1]
, is a polynomial in 1/z used to expand functions in term of Bessel functions.[1]
The first few polynomials are
A general form for the polynomial is
they have the generating function
where J are Bessel functions.
To expand a function f in form
for 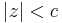 compute
compute
where 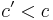 and c is the distance of the nearest singularity of
and c is the distance of the nearest singularity of 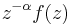 from
from 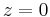 .
.
Examples
An example is the extension
or the more general Sonine formula[2]
where 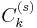 is Gegenbauer's polynomial. Then,
is Gegenbauer's polynomial. Then,
the confluent hypergeometric function
and in particular
the index shift formula
the Taylor expansion (addition formula)
(cf. [3]) and the expansion of the integral of the Bessel function
are of the same type.
See also
Notes
- ^ Abramowitz and Stegun, p. 363, 9.1.82 ff.
- ^ Erdélyi et al. 1955 II.7.10.1, p.64
- ^ I.S. Gradshteyn (И.С. Градштейн), I.M. Ryzhik (И.М. Рыжи); Alan Jeffrey, Daniel Zwillinger, editors. Table of Integrals, Series, and Products, seventh edition. Academic Press, 2007. ISBN 978-0-12-373637-6. Equation 8.515.1